NCERT Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments - Param Himalaya
9.1 A small candle. 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirroг should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
Solution:
Here , h = 2.5 cm , u = - 27 cm , R = - 36 cm
Since $f = \frac{R}{2}$ .
Therefore, $f = \frac{-36}{2}$ = -18 cm
(i) using mirror formula
$\frac{1}{u} + \frac{1}{v} = \frac{1}{f}$ , we get
$\frac{1}{v} = \frac{1}{f} - \frac{1}{u}$
$\frac{1}{v} = \frac{1}{(-18)} - \frac{1}{(-27)}$
$\frac{1}{v} = -\frac{1}{18} + \frac{1}{27}$
$\frac{1}{v} = \frac{-3+2}{54}$
$\frac{1}{v} = -\frac{1}{54}$
$v = - 54 cm$ ( Position of image )
Thus , the screen should be placed at a distance of 54 cm in front of the concave mirror.
(ii) Using , $\frac{h{'}}{h} = - \frac{v}{u}$ , we get
$h{'} = - \frac{v}{u}h$
$h{'}= - \frac{-54 cm}{-27 cm} \times 2.5 cm$
$h{'} = -5.0 cm$
Thus , size of image is 5.0 cm
Nature of image : Real , inverted and magnified.
When the candle is moved closer to the mirror, the image will move away from the mirror and likewise, the screen has to be moved away to bring the image on the screen. However, when the candle is at a distance less than 18 cm, the image formed will be virtual. In that situation, the image cannot be brought to the screen.
9.2 A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification.Describe what happens as the needle is moved farther from the mirror.
Solution:
here , $h_{1} = 4.5 cm$ , u = -12 cm , f = 15 cm
Using
$\frac{1}{u} + \frac{1}{v} = \frac{1}{f}$ , we get
Or $\frac{1}{v} = \frac{1}{f} - \frac{1}{u}$
$\frac{1}{v} = \frac{1}{15} - \frac{1}{(-12)}$
Or $\frac{1}{v} = \frac{1}{15} + \frac{1}{12}$
$\frac{1}{v} = \frac{4+5}{60}$
$\frac{1}{v} = \frac{9}{60}$
Or $v = \frac{60}{9}$ cm
v = 6.7 cm
Thus , the image is formed at 6.7 cm behind the mirror As magnification
$m = \frac{h{'}}{h} = -\frac{v}{u}$ , we get
$\frac{h{'}}{4.5} = \frac{-\frac{60}{9}}{-12} =\frac{5}{9}$
$h{'} = \frac{5 \times 4.5}{9} = 2.5 cm$ ( size of image)
Magnification
$m= \frac{2.5}{4.5}$
$m= \frac{25}{45}$
$m= \frac{5}{9}$
$m= 0.55$
Thus , the image is virtual, erect and diminished. As we move the needle away from the mirror , the image goes on decreasing in size and moves towards the principal focus on the other side.
9.3 A tank is filled with water to a height of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 9.4 cm. What is the refractive index of water? If water is replaced by a liquid of refractive index 1.63 up to the same height, by what distance would the microscope have to be moved to focus on the needle again?
Solution:
Here , real depth = 12.5 , Apparent depth = 9.4cm
Using ,
$n_{wa} = \frac{real \:depth}{Apparent \: depth}$
we get
$n_{wa} =\frac{12.5}{9.4}$
$n_{wa} = 1.33$
If water is replaced by liquid , then
$n_{la} = 1.63$
$n_{la} = \frac{real \:depth}{Apparent \: depth}$
So
$apparent \: depth = \frac{real \: depth}{n_{la}}$
$apparent \: depth=\frac{12.5}{1.63} = 7.66 cm$
$\therefore$ Distance through which the microscope has to be moved = $9.4-7.66 = 1.74 cm$
9.4 Figures 9.27(a) and (b) show refraction of a ray in air incident at 60° with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in glass when the angle of incidence in water is 45° with the normal to a water-glass interface [Fig. 9.27(c)].
9.5 A small bulb is placed at the bottom of a tank containing water to a depth of 80cm. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. (Consider the bulb to be a point source.)
Solution:
9.6 A prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism? The refracting angle of the prism is 60°. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.
Solution:
9.7 Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length. is to be 20cm?
Solution:
$$\frac{1}{f} = (\mu-1)\left ( \frac{1}{R_{1}} -\frac{1}{R_{2}}\right )$$
$$\frac{1}{20} = (1.55-1)\left ( \frac{1}{R} -\frac{1}{(-R)}\right )$$
$$\frac{1}{20} = (0.55)\left ( \frac{1}{R} +\frac{1}{R}\right )$$
$$\frac{1}{20} = 0.55 \times \frac{2}{R}$$
$$R= 1.1 \times 20$$
$$R=22cm$$
9.8 A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12cm from P. At what point does the beam converge if the lens is (a) a convex lens of focal length 20cm, and (b) a concave lens of focal length 16cm?
Solution:
(a) Here point P on the right of the lens acts as a virtual object.
Now , u = +12 cm ; f =+ 20 cm ; v= ?
$$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$$
$$\frac{1}{v} - \frac{1}{12} = \frac{1}{20}$$
$$\frac{1}{v} = \frac{1}{20}+\frac{1}{12}$$
$$\frac{1}{v} = \frac{3+5}{60}$$
$$\frac{1}{v} = \frac{8}{60}$$
$$v = \frac{60}{8}$$
$$v = 7.5 cm$$
Here v is positive, Therefore, the beam converges at a point 7.5 cm to the right of lens.
(b) Here Point P on the right of the lens acts as a virtual object.
Now , u = +12 cm ; f =-16 cm ; v= ?
$$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$$
$$\frac{1}{v} - \frac{1}{12} = \frac{1}{-16}$$
$$\frac{1}{v} = \frac{1}{12}+\frac{1}{-16}$$
$$\frac{1}{v} = \frac{4-3}{48}$$
$$\frac{1}{v} = \frac{1}{48}$$
$$v = 48 cm$$
Again v is positive, Therefore the beam converges at the points 48 cm to the right of the lens.
9.9 An object of size 3.0cm is placed 14cm in front of a concave lens of focal length 21 cm. Describe the image produced by the lens. What happens if the object is moved further away from the lens?
Solution:
Given
$h_{1}$ = 3 cm , u = -14 cm , f = -21 cm , v= ?
$$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$$
$$\frac{1}{v} = \frac{1}{u} + \frac{1}{f}$$
$$\frac{1}{v} = \frac{1}{(-14)} + \frac{1}{(-21)}$$
$$\frac{1}{v} = -\frac{1}{14}-\frac{1}{21}$$
$$\frac{1}{v} = -(\frac{1}{14}+\frac{1}{21})$$
$$\frac{1}{v} =-( \frac{3+2}{42})$$
$$\frac{1}{v} =- \frac{5}{42}$$
$$v =- \frac{42}{5}$$
$$v =- 8.4 cm$$
v is negative, therefore, the image is virtual , erect and is formed at 8.4 cm from the lens on the same side as the object.
Now .
$$m =\frac{h_{2}}{h_{1}}= \frac{v}{u}$$
$$h_{2}=h_{1} \times \frac{v}{u}$$
$$h_{2}= 3 \times \frac{-8.4}{-14}$$
$$h_{2}= 1.8 cm$$
The image is diminished in size , as the object is moved away from the lens , the virtual image moves towards the focus of the lens ( but never beyond it ) and progressively decrease in size.
9.10 What is the focal length of a convex lens of focal length 30cm in contact with a concave lens of focal length 20cm? Is the system a converging or a diverging lens? Ignore thickness of the lenses.
Solution:
Focal length of convex lens= $f_{1}$= +30cm
Power of convex lens = $P_{1} = \frac{1}{f_{1}}$
Focal length of concave lens = $f_{2}$= -20cm
Power of concave lens = $P_{2}= \frac{1}{f_{2}}$
Power of combination of lenses is
$$P= P_{1}+P_{2}$$
$$\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}$$
$$\frac{1}{f}=\frac{1}{30}+\frac{1}{-20}$$
$$\frac{1}{f}=\frac{1}{30}-\frac{1}{20}$$
$$\frac{1}{f}=\frac{2-3}{60}=-\frac{1}{60}$$
$$f= -60cm$$
Therefore f=-60cm As a result, the focal length of the lens combination is 60cm. In addition, the negative sign indicates that the lens system in use is a diverging lens.
9.11 A compound microscope consists of an objective lens of focal length 2.0cm and an eyepiece of focal length 6.25cm separated by a distance of 15cm. How far from the objective should an object be placed in order to obtain the final image at (a) the least distance of distinct vision (25cm), and (b) at infinity? What is the magnifying power of the microscope in each case?
Solution:
Here $f_{o} = 2.0 cm$ , $f_{e} = 6.25 cm$ , $u_{o} = ?$
(a) Final image at the least distance of distinct vision :
The least distance of distinct vision (D) is 25 cm
For eye lens :
$$\frac{1}{v_{e}} - \frac{1}{u_{e}} = \frac{1}{f_{e}}$$
Here , $v_{e} = -25cm$ , $f_{e} = +6.25 cm$ , $u_{e} =?$
$$\frac{1}{-25} - \frac{1}{u_{e}} = \frac{1}{6.25}$$
$$\frac{1}{u_{e}} = -\frac{1}{25} - \frac{4}{25}$$
$$\frac{1}{u_{e}} = -(\frac{1}{25}+\frac{4}{25})$$
$$\frac{1}{u_{e}} = - \frac{(1+4)}{25}$$
$$\frac{1}{u_{e}} = - \frac{5}{25}$$
$$u_{e} = - \frac{25}{5}$$
$$u_{e} = - 5 cm$$
For objective lens :
$$\frac{1}{v_{o}} - \frac{1}{u_{o}} = \frac{1}{f_{o}}$$
Here ,
$$v_{o} = L - u_{e}$$
$$v_{o}= 15-5= 10cm$$
$$f_{o} = +2 cm$$
$$\frac{1}{v_{o}} - \frac{1}{u_{o}} = \frac{1}{f_{o}}$$
$$\frac{1}{u_{o}} = \frac{1}{v_{o}} - \frac{1}{f_{o}}$$
$$\frac{1}{u_{o}} = \frac{1}{10} - \frac{1}{2}$$
$$\frac{1}{u_{o}} = \frac{1-5}{10}$$
$$\frac{1}{u_{o}} = \frac{-4}{10}$$
$$u_{o} = -2.5cm$$
Therefore , distance of the object from the objectives is 2.5 cm. Magnifying power of the microscope under this condition is
$$M = \frac{v_{o}}{u_{o}} (1+ \frac{D}{f_{o}})$$
$$M= \frac{10}{-2.5} (1+ \frac{25}{6.25})$$
$$M= -4 (1+4)$$
$$M = -4 \times 5$$
$$M = -20$$
The negative sign shows that the final image obtained is inverted w.r.t the object.
(b) Final image at infinity:
$$\frac{1}{v_{e}} - \frac{1}{u_{e}} = \frac{1}{f_{e}}$$
$$\frac{1}{ \infty } - \frac{1}{u_{e}} = \frac{1}{6.25}$$
$$0 - \frac{1}{u_{e}} = \frac{1}{6.25}$$
$$- \frac{1}{u_{e}} = \frac{1}{6.25}$$
$$u_{e} = -6.25$$
Final image will be formed at infinity if the objectives lens forms the image of the object at the focus of the eyes lens i.e at a distance of 6.25 cm from the eye lens.
$$v_{o} = L - f_{e}$$
$$v_{o} = 15 - 6.25 = +8.75cm$$
$$\frac{1}{v_{o}} - \frac{1}{u_{O}} = \frac{1}{f_{o}}$$
$$\frac{1}{8.75} - \frac{1}{u_{o}} = \frac{1}{2}$$
$$\frac{1}{u_{o}} = \frac{1}{8.75} - \frac{1}{2}$$
$$\frac{1}{u_{o}} = \frac{2-8.75}{17.5}$$
$$\frac{1}{u_{o}} = \frac{-6.75}{17.5}$$
$$u_{o} = -\frac{17.5}{6.75}$$
$$u_{o} = -2.59 cm$$
Therefore, distance of the object from the objective is 2.59cm. magnifying power of the microscope under this condition is
$$M = \frac{v_{o}}{u_{o}} \times \frac{D}{f_{o}}$$
$$M = \frac{8.75}{-2.59} \times \frac{25}{6.25}$$
$$M= -13.51$$
9.12 A person with a normal near point (25cm) using a compound microscope with objective of focal length 8.0 mm and an eyepiece of focal length 2.5cm can bring an object placed at 9.0mm from the objective in sharp focus. What is the separation between the two lenses? Calculate the magnifying power of the microscope.
Solution:
Here
$D = 25 cm$
$f_{o}= 8.0 mm = 0.8cm$
$f_{e} = 2.5 cm$
For objective lens :
$u_{o} = -9mm= -0.9cm$
$$\frac{1}{v_{o}} - \frac{1}{u_{o}} = \frac{1}{f_{o}}$$
$$\frac{1}{v_{o}} - \frac{1}{-0.9} = \frac{1}{0.8}$$
$$\frac{1}{v_{o}} = \frac{1}{0.8} - \frac{1}{0.9}$$
$$\frac{1}{v_{o}} = \frac{0.9-0.8}{0.72}$$
$$\frac{1}{v_{o}} = \frac{0.1}{0.72}$$
$${v_{o}} = \frac{0.72}{0.1}$$
$${v_{o}} = 7.2cm$$
For eye lens :
$v_{e} = -D = -25 cm$
$$\frac{1}{v_{e}} - \frac{1}{u_{e}} = \frac{1}{f_{e}}$$
$$\frac{1}{-25} - \frac{1}{u_{e}} = \frac{1}{2.5}$$
$$\frac{1}{u_{e}} = \frac{1}{-25} - \frac{1}{2.5}$$
$$\frac{1}{u_{e}} = -( \frac{1}{25} +\frac{1}{2.5})$$
$$\frac{1}{u_{e}} = -( \frac{1}{25} +\frac{1}{2.5})$$
$$\frac{1}{u_{e}} = -\frac{1+10}{25}$$
$$\frac{1}{u_{e}} = -\frac{11}{25}$$
$$u_{e} = -\frac{25}{11}$$
$$u_{e} = -2.27cm$$
So separation between two lens
$$L= |u_{e}|+ |v_{0}|$$
$$L = 2.27+7.2$$
$$L = 9.47 cm$$
Magnifying power ,
$$M = \frac{v_{o}}{u_{o}} \times(1+ \frac{D}{f_{o}})$$
$$M = \frac{7.2}{-0.9} \times(1+ \frac{25}{2.5})$$
$$M = -88$$
9.13 A small telescope has an objective lens of focal length 144cm and an eyepiece of focal length 6.0cm. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece?
Solution:
Here $f_{0}= 144 cm$ , $f_{e}= 6 cm$
When the final image is formed at infinity , the telescope is said to be in normal adjustment.
it's magnifying power is
$$M = \frac{f_{0}}{f_{e}} = \frac{144}{6}$$
$$M = 24$$
Separation between the objective and eyepiece is
$$L = f_{o} + f_{e}$$
$$L = 144+6$$
$$L = 150cm$$
9.14 (a) A giant refracting telescope at an observatory has an objective lens of focal length 15m. If an eyepiece of focal length 1.0cm is used, what is the angular magnification of the telescope?
(b) If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is $3.48 \times 10^{6}m$ and the radius of lunar orbit is $3.8 \times 10^{8} m$
Solution:
$f_{0} = 15 m$ , $f_{e} = 1 cm = 0.01 m$
(a) Angular magnification
$$M= \frac{f_{o}}{f_{e}} $$
$$M= \frac{15}{0.01} = 1500$$
(b) The angle subtended by the moon is
$$\alpha = \frac{D}{L}$$
$$\alpha = \frac{3.48 \times 10^{6}}{3.8 \times 10^{8}}$$
Let d be the diameter of the image of the moon . Now angle subtended by the image formed by the objective will also be equal to $\alpha$ and is given by
$$\alpha = \frac{d}{f_{0}}$$
$$\alpha = \frac{d}{15}$$
$$\frac{d}{15} = \frac{3.48 \times 10^{6}}{3.8 \times 10^{8}}$$
$$d = 15 \times \frac{3.48 \times 10^{6}}{3.8 \times 10^{8}}$$
$$d =13.73 \times 10^{-2}m$$
$$d=13.73cm$$
9.15 Use the mirror equation to deduce that:
(a) an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
(b) a convex mirror always produces a virtual image independent of the location of the object.
(c) the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.
(d) an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.
Solution:
(a) Given that the object is placed between f and 2f
2f<u<f for u<0 , f<0
From mirror formula
$$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$$
$$v= \frac{uf}{u-f}$$
For a concave mirror , f is -ve and u is always -ve
Since
$$v = \frac{(-ve)(-ve)}{(-ve)-(-ve)}$$
$$v = \frac{(-ve)(-ve)}{(-ve+ve)}$$
|u|>|f|
So
$$v = \frac{+ve}{-ve}$$
$$v = -ve$$
since v is negative , the image is formed on the left side.
From the mirror formula
$$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$$
$$v = \frac{uf}{u-f}$$
If u= -f
$$v= \frac{(-f)(-f)}{-f-(-f)} = \infty$$
If u = -2f
$$v = \frac{(-2f)(-f)}{-2f-(-f)}$$
v = -2f
So
$$\infty<v<2f<u<f$$
Hence the image will be formed beyond 2f on left side
Now
$$M = -\frac{v}{u}$$
$$M = - \frac{-ve}{-ve}$$
$$M = - ve$$
Since image will be real
Since |v|>|u|
So |m|>1
So image will be inverted
(b)
From the mirror formula
$$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$$
$$v = \frac{uf}{u-f}$$
For convex mirror f>0 and u<0
So
$$v = \frac{(-ve)(+ve)}{(-ve)-(+ve)}$$
$$v = \frac{-ve}{-ve}$$
$$v = +ve$$
Since v is positive, the image is formed behind the mirror i.e. the image is virtual whatever may be the value of u.
(c)
From the mirror formula
$$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$$
$$v = \frac{uf}{u-f}$$
For convex mirror f>0 and u<0
So
$$v = \frac{(-ve)(+ve)}{(-ve)-(+ve)}$$
$$v = \frac{-ve}{-ve}$$
$$v = +ve$$
Magnification
m = - \frac{v}{u} = \frac{f}{f-u}
Since f>0 , u<0
M = \frac{+ve}{+ve-(-ve)}
M = +ve
Thus image formed virtual and erect
If |u|>|f|
Then |M|<1
Thus image formed is diminished in size
From the mirror formula
$$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$$
$$\frac{1}{v} = \frac{1}{f} - \frac{1}{u}$$
As u<0
$$\frac{1}{v} > \frac{1}{f}$$
v<f
Thus , the image produced is diminished in size and located between pole and focus.
(d) Now f <0, u<0 and f<u<0
From the mirror formula
$$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$$
$$v = \frac{uf}{u-f}$$
$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$
$v = \frac{uf}{u-f}$
$v= \frac{(-ve)(-ve)}{(-ve)-(-ve)}$
If |u|<|f|
Then
$v = \frac{+ve}{+ve}$
v = +ve
Now
$M = -\frac{v}{u}$
$M = - \frac{\frac{uf}{u-f}}{u}$
$M = - \frac{f}{u-f}$
$M = - \frac{-ve}{(-ve)-(-ve)}$
If |u|<|f|
$M = - \frac{-ve}{+ve}$
M = +ve
Also
M>1
Since v is positive and m>1 , virtual and enlarged image will be formed.
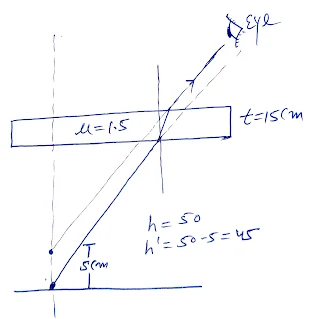
9.16 A small pin fixed on a table top is viewed from above from a distance of 50cm. By what distance would the pin appear to be raised if it is not viewed from the same point through a 15cm thick glass slab held parallel to the table? Refractive index of glass = 1.5. Does the answer depend on the location of the slab?
Solution:
$$\mu_{ga} = \frac{Real \ Depth}{Apparent \ Depth}$$
$$1.5 = \frac{15}{A.D}$$
$$A.D = \frac{15}{1.5}$$
$$A.D = 10cm$$
Distance by which pin appear to be raised (Normal shift ) = R.D - A.D
d = 15-10 = 5 cm
The answer does not depend on the location of the glass slab.
9.17 (a) Figure 9.28 shows a cross-section of a light pipe made of a glass fibre of refractive index 1.68, The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.
(b) What is the answer if there is no outer covering of the pipe?
Solution:
Here
$\mu_{1} = 1.44 , \mu_{2} = 1.68$
(a) Let C be the critical angle of the fibre material with respect to material of outer coating.
$$_{1}\mu_{2} = \frac{\mu_{2}}{\mu_{1}}$$
$$_{1}\mu_{2} = \frac{1.68}{1.44}$$
$$_{1}\mu_{2} = 1.167$$
The critical angle C is given by :
$$sin C = \frac{1}{_{1}\mu_{2}} = \frac{1}{1.167}$$
$$sinC = 0.8569$$
$$C = sin^{-1}0.8569$$
$$C = 59^{o}$$
Total internal reflection will occurs if the angle of incidence at the glass fibre coating interface is equal to or greater than the critical angle C = 59° thus are will be maximum when angle of incidence C = 59°
$$r_{max} = 90^{o} - C $$
$$r_{max} = 90^{o} - 59^{o} =31^{o}$$
By snell's law ,
$$\frac{sini_{max}}{sinr_{max}} = 1.68$$
$$sini_{max} = 1.68 \times sinr_{max}$$
$$sini_{max} = 1.68 \times sin31^{o}$$
$$sini_{max} = 1.68 \times 0.5150$$
$$sini_{max} = 0.8662$$
$$i_{max} = sin^{-1}0.8662$$
$$i_{max} = 60^{o}$$
Thus all the incident ray which make angles in the range between zero degree and 60 degree with the axis of the pipe will suffer total internal reflection in the pipe
(b) If there is no outer coating of pipe
$\mu_{2}=1.68 , \mu_{1} = 1$
Now
$$sin C^{'} = \frac{1}{_{1}\mu_{2}} = \frac{1}{1.68}$$
$$sin C^{'} = 0.5952$$
$$C^{'} = sin^{-1}0.5952$$
$$C^{'} = 36.5^{o}$$
For $i = 0^{o}$ , $r = 0^{o}$ , Therefore,
$$i^{'} = 90^{o} -r$$
$$i^{'} = 90^{o} - 0 = 90^{o}$$
Which is greater than $C^{'}$. So the ray of light incident at $0^{o}$ will undergo total internal reflection.
For $i = 90^{o}$
$$\frac{sini}{sinr} =1.68$$
$$\frac{sin90^{o}}{sinr} =1.68$$
$$sinr =\frac{1}{1.68}$$
$$r = 36.5^{o}$$
$$C =90^{o}-36.5^{o} = 53.5^{o}$$
Which is greater than $C^{'}$.
Thus when there is no outer coating of the pipe , all the rays incident at angles in the range $0^{o}$ to $90^{o}$ will suffer total internal reflection.
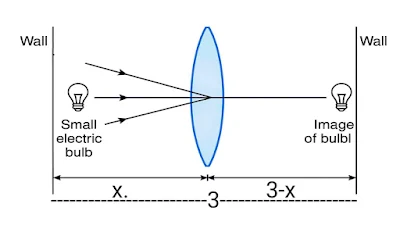
9.18 The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 3m away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?
Solution :
Given that , the separation between object and the image is 3 m .
Let the object distance from the lens be x , this implies that the image distance is 3-x.
Let the required focal length be f.
u = -x
v = 3-x
From the lens formula
$$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$$
$$\frac{1}{3-x} - \frac{1}{(-x)} = \frac{1}{f}$$
$$\frac{1}{3-x} + \frac{1}{x} = \frac{1}{f}$$
$$\frac{3-x+x}{x(3-x)} = \frac{1}{f}$$
$$\frac{3}{3x-x^{2}} = \frac{1}{f}$$
$$f = \frac{3x-x^{2}}{3}$$
$$f = x - \frac{x^{2}}{3}$$
To find the maximum of f ,
$$\frac{df}{dx} = 0$$
$$\frac{d}{dx}(x - \frac{x^{2}}{3}) = 0$$
$$1- \frac{2x}{3} = 0$$
$$x = \frac{3}{2}m$$
Then
$$f = x - \frac{x^{2}}{3}$$
$$f = \frac{3}{2} - \frac{(\frac{3}{2})^{2}}{3}$$
$$f = \frac{3}{2} - \frac{3}{4}$$
$$f = \frac{6-3}{4}$$
$$f = \frac{3}{4}$$
$$f = 0.75 m$$
Alternative method :
The min distance between an object & it's real image (convex lens ) is 4f.
$$D = 4f_{max}$$
$$f_{max} = \frac{D}{4}$$
$$f_{max} = \frac{3}{4}$$
$$f_{max} = 0.75 m$$
9.19 A screen is placed 90cm from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20cm. Determine the focal length of the lens.
Solution :
Case 1. When the lens is at position $L_{1}$
u = -x
v = 90-x
Then lens formula :
$$\frac{1}{f} = \frac{1}{v} - \frac{1}{u}$$
$$\frac{1}{f} = \frac{1}{90-x} - \frac{1}{(-x)}$$
$$\frac{1}{f} = \frac{1}{90-x}+ \frac{1}{x}$$
$$\frac{1}{f} = \frac{x+90-x}{(90-x)(x)}$$
$$\frac{1}{f} = \frac{90}{(90x-x^{2})} ....(i)$$
case 2. when the lens is at position $L_{2}$ :
u = -(x+20)
v = (70-x)
Then lens formula :
$$\frac{1}{f} = \frac{1}{v} - \frac{1}{u}$$
$$\frac{1}{f} = \frac{1}{70-x} - \frac{1}{-(x+20)}$$
$$\frac{1}{f} = \frac{1}{70-x} + \frac{1}{(x+20)}$$
$$\frac{1}{f} = \frac{x+20+70-x}{(70-x)(x+20)}$$
$$\frac{1}{f} = \frac{90}{70x+1400-x^{2}-20x}$$
$$\frac{1}{f} = \frac{90}{50x+1400-x^{2}}......(ii)$$
From equation (i) and (ii)
$$ \frac{90}{(90x-x^{2})} = \frac{90}{50x+1400-x^{2}}$$
$$\frac{90}{(90x-x^{2})} = \frac{90}{50x+1400-x^{2}}$$
$$(90x-x^{2}) = 50x+1400-x^{2}$$
$$40x = 1400$$
$$x = \frac{1400}{40}$$
$$x= \frac{70}{2}$$
x$$= 35cm$$
So u = -x = -35 cm , v = 90-x = 55
Then lens formula
$$\frac{1}{f} = \frac{1}{55} - \frac{1}{(-35)}$$
$$\frac{1}{f} = \frac{1}{55} + \frac{1}{35}$$
$$\frac{1}{f} = \frac{55+35}{35 \times 55}$$
$$\frac{1}{f} = \frac{7+11}{385}$$
$$\frac{1}{f} = \frac{18}{385}$$
$$f = \frac{385}{18}$$
$$f = 21.4 cm$$
9.20 (a) Determine the effective focal length of the combination of the two lenses in Exercise 9.10. if they are placed 8.0cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident? Is the notion of effective focal length of this system useful at all?
(b) An object 1.5 cm in size is placed on the side of the convex lens in the arrangement (a) above. The distance between the object and the convex lens is 40cm. Determine the magnification. produced by the two-lens system, and the size of the image.
Solution :
(a) If two lenses of focal lengths $f_{1}$ and $f_{2}$ are placed d distance apart , then equivalent effective focal length ( F) of the combination is given by :
$$\frac{1}{F} = \frac{1}{f_{1}} + \frac{1}{f_{2}} - \frac{d}{f_{1}.f_{2}}$$
Here , $f_{1} = +30cm$ , $f_{2}=-20cm$ , d = 8 cm
$$\frac{1}{F} = \frac{1}{30} + \frac{1}{(-20)} - \frac{8}{(30)(-20)}$$
$$\frac{1}{F} = \frac{1}{30} + \frac{1}{(-20)} - \frac{8}{(30)(-20)}$$
$$\frac{1}{F} = \frac{1}{30}- \frac{1}{20}+ \frac{1}{75}$$
$$\frac{1}{F} = -\frac{1}{300}$$
$$F = -300cm$$
(i) When parallel beam of light falls on convex lens first :
Let the parallel beam of light be incident on the convex lens first. If the second lens ( concave lens ) is absent , then
$$u_{1} = \infty , f_{1} = +30 cm$$
Now
$$ \frac{1}{v_{1}} = \frac{1}{u_{1}} + \frac{1}{f_{1}}$$
$$\frac{1}{v_{1}} = \frac{1}{\infty} + \frac{1}{30}$$
$$\frac{1}{v_{1}} =\frac{1}{30}$$
$$v_{1} = 30cm$$
When the concave lens is also present , this image would act as virtual object for the concave lens.
$$u_{2} = +(30-8) = +22cm$$
$$f_{2} = -20 cm$$
$$\frac{1}{v_{2}} = \frac{1}{u_{2}}+ \frac{1}{f_{2}}$$
$$\frac{1}{v_{2}} = \frac{1}{22}+ \frac{1}{-20}$$
$$\frac{1}{v_{2}} = \frac{1}{22}- \frac{1}{20}$$
$$\frac{1}{v_{2}} = -\frac{1}{220}$$
$$v_{2} = - 220 cm$$
This a parallel beam of light would appear to diverse from a point 220-4 = 216 cm from the centre of the system of two lenses.
(ii) When parallel beam of light falls on concave lens first :
Let the parallel beam of light incident on the concave lens first.
$$u_{1} = \infty , f_{1} = -20 cm$$
$$ \frac{1}{v_{1}} = \frac{1}{u_{1}} + \frac{1}{f_{1}}$$
$$\frac{1}{v_{1}} = \frac{1}{\infty} + \frac{1}{(-20)}$$
$$\frac{1}{v_{1}} =-\frac{1}{20}$$
$$v_{1} =- 20cm$$
This image would act as a virtual object for the second lens.
$$u_{2} = -(20+8) = -28cm$$
$$f_{2} = +30cm$$
$$\frac{1}{v_{2}} = \frac{1}{u_{2}}+ \frac{1}{f_{2}}$$
$$\frac{1}{v_{2}} = \frac{1}{-28}+ \frac{1}{+30}$$
$$\frac{1}{v_{2}} = \frac{-15+14}{420}$$
$$\frac{1}{v_{2}} = -\frac{1}{420}$$
$$v_{2} = - 420 cm$$
Thus a parallel beam of light would appear to diverse from a point 420-4 = 416 cm from the centre of the two lens system .
The above calculation shows that the answer depends on which side of the lens The parallel beam of light is incident therefore the notation of effective focal length does not seen to be useful for the system.
(b) Here the object is placed on the side of the convex lens.
$u_{1} = -40 cm$ , $f_{1} = +30 cm$ , $h_{1} = 1.5 cm$
$$ \frac{1}{v_{1}} = \frac{1}{u_{1}} + \frac{1}{f_{1}}$$
$$\frac{1}{v_{1}} = \frac{1}{(-40)} + \frac{1}{30}$$
$$\frac{1}{v_{1}} =-\frac{-3+4}{120}$$
$$v_{1} = 120$$
Magnification produced by the convex lens is
$$m_{1} = - \frac{v_{1}}{u_{1}} = \frac{120}{-40}$$
$$m_{1} = 3$$
Now the image formed by the convex lens act as a virtual object for the second lens (concave lens)
$$u_{2} = +(120-8) = +112 cm , f_{2} = -20 cm \frac{1}{v_{2}} = \frac{1}{u_{2}} + \frac{1}{f_{2}}$$
$$\frac{1}{v_{2}} = \frac{1}{112} + \frac{1}{-20}$$
$$\frac{1}{v_{2}} = \frac{20-112}{112 \times 20} = \frac{-92}{112 \times 20}$$
$$v_{2} =- \frac{112 \times 20}{92}$$
$$v_{2} = - 24.34 cm$$
Magnification produced by the second lens is
$$m_{2} = - \frac{v_{2}}{u_{2}}$$
$$m_{2} = - \frac{-24.3}{112}$$
$$m_{2} =0.2173$$
Magnification produced by the lens system is
$$m = m_{1} \times m_{2}$$
$$m = 3 \times 0.2173 = 0.652$$
Size of image ,
$$h_{2} = m. h_{1} = 0.652 \times 1.5$$
$$h_{2}= 0.98 cm$$
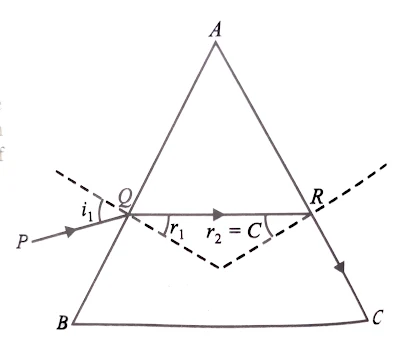
9.21 At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524.
Solution :
Here A = 60° , $\mu=1.544$ , i = ?
Here Ray of light PQ incident on the face ab will just suffer total internal reflection at the other face AC if it is incident on the face AC at an angle equal to the critical angle C for the material of the prism
$$r_{2} = C$$
$$sin C = \frac{1}{ \mu} = \frac{1}{1.524}$$
$$sin C = 0.6562$$
C = 41°
Now , for a prism ,
$$r_{1} + r_{2} = A$$
$$r_{1} = A -r_{2}$$
$$r_{1} = A - C$$
$$r_{1} = 60^{o} - 41^{o}$$
$$r_{1} = 19^{o}$$
Applying snell's law at face AB , we have
$$\frac{sini_{1}}{sinr_{1}} = \mu$$
$$\frac{sini_{1}}{sin19^{o}} = 1.524$$
$$sini_{1} = 1.524 \times sin 19^{o}$$
$$sini_{1} = 0.4962$$
$$i_{1} = sin^{-1}0.4962$$
$$i_{1} = 29.75^{0}$$
9.22 A card sheet divided into squares each of size 1 mm² is being viewed at a distance of 10 cm through a magnifying glass (a converging lens of focal length 9 cm) held close to the eye.
(a) What is the magnification produced by the lens? How much is the area of each square in the virtual image?
(b) What is the angular magnification (magnifying power) of the lens?
(c) Is the magnification in (a) equal to the magnifying power in (b)? Explain.
Solution :
Here u = -9cm , f = +10cm
Area of each square (object) = $1 mm \times 1mm = 1 mm^{2}$
(a) Linear magnification produced by the lens is
$$m = \frac{v}{u}$$
For a lens
$$\frac{1}{v} = \frac{1}{f} + \frac{1}{u}$$
$$\frac{1}{v} = \frac{1}{10} + \frac{1}{-9}$$
$$\frac{1}{v} = \frac{1}{10} - \frac{1}{9}$$
$$\frac{1}{v} = \frac{9-10}{90}$$
$$\frac{1}{v} = -\frac{1}{90}$$
$$v = - 90 cm$$
$$m = \frac{v}{u}$$
$$m = \frac{90}{9}$$
$$m = 10$$
Since the lens produces linear magnification, area of each square in the image = $1 mm \times 10 \times 1 mm \times 10 = 100mm^(2)$
(b) Angular magnification ( magnifying power ) of the lens is
$$M = \frac{D}{u} = \frac{25}{9} = 2.8$$
(c) No, The magnification produced by a lens in part (a) is v/u while the magnifying power of the lens is part (b) is D/u. Obviously, the two are not equal unless v = D i. e the image is formed at the least distance of distinct vision.
9.23 (a) At what distance should the lens be held from the card sheet in Exercise 9.22 in order to view the squares distinctly with the maximum possible magnifying power?
(b) What is the magnification in this case?
(c) Is the magnification equal to the magnifying power in this case.Explain.
Solution :
(a) Maximum magnifying power is obtained when the image is formed at the least distance of distinct vision (i.e at D = 25 cm )
For a lens
$$\frac{1}{u} = \frac{1}{v} - \frac{1}{f}$$
Here , v = -D = -25 cm
f = +10 cm , u = ?
$$\frac{1}{u} = \frac{1}{-25} - \frac{1}{10}$$
$$\frac{1}{u} = -\frac{1}{25}-\frac{1}{10}$$
$$\frac{1}{u} = \frac{-2-5}{50}$$
$$\frac{1}{u} = \frac{-7}{50}$$
$$u = - \frac{50}{7}$$
$$u= -7.14 cm$$
Therefore, the lens should be held 7.14 cm away from the figure
(b) Magnitude of magnification (linear) is
$$m = \frac{v}{u} = \frac{-25}{50/7}
$$m = 3.5$$
(c) When the object is so placed that the image is formed at the least distance of distinct vision , the magnifying power is
$$m = \frac{D}{u}$$
$$m = \frac{-25}{-50/7}$$
$$m = 3.5$$
Therefore the answer of part c is yes. Magnification (linear) and magnify power of lens are equal when the image is formed at the least distance of distinct vision (25cm).
9.24 What should be the distance between the object in Exercise 9.23 and the magnifying glass if the virtual image of each square in the figure is to have an area of 6.25 mm². Would you be able to see the squares distinctly with your eyes very close to the magnifier?
[Note: Exercises 9.22 to 9.24 will help you clearly understand the difference between magnification in absolute size and the angular. magnification (or magnifying power) of an instrument.]
Solution :
Object area = $1 mm^{2}$
Image area = $6.25 mm^{2}$
Areal Magnification =$\frac{6.25}{1} = 6.25$
Linear magnification =
$$m = \sqrt{6.25}$$
$$m = \frac{v}{u}$$
$$v = mu$$
$$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$$
$$\frac{1}{2.5u} - \frac{1}{u} = \frac{1}{10}$$
$$\frac{1-2.5}{2.5u} = \frac{1}{10}$$
$$2.5u = -15$$
$$u = -6 cm$$
Also , $v = mu = 2.5 \times (-6) = -15 cm$
9.25 Answer the following questions:
(a) The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification?
(b) In viewing through a magnifying glass, one usually positions one's eyes very close to the lens. Does angular magnification change if the eye is moved back?
(c) Magnifying power of a simple microscope is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal length and achieving greater and greater magnifying power?
(d) Why must both the objective and the eyepiece of a compound microscope have short focal lengths?
(e) When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why? How much should be that short distance between the eye and eyepiece?
Solution :
(a) It is true that angular size of the image is equal to the angular size of the object when magnifying glass is not used , an object has to be placed at distance of 25 cm(D) but the use of magnifying glass allows up to place the object much closer to the eye then 25 cm. Obviously the angle formed by the object at the eye when it is closer to the eye will be larger than the angle formed by it when place 25 cm from the eye it is in this sense that are magnify glass produce angular magnification.
(b) Yes , the angle magnification decrease slightly if the eye moved back. It is because now the angles subtended at the eye by the image is less than that subtended by the image at the lens. This effect is negligible when the image is at much larger distance.
(c) This is due to two principal reasons first a lens of short focal length is not easy to manufacture. Secondly the more importantly. When we decrease the focal length both spherical and the chromatic aberrations become large. Therefore, in practice, we cannot get a magnifying glass of power more than 3D or so.
(d) The magnify power of a compound microscope is given by
$$M = \frac{L}{f_{o}}(1+\frac{D}{f_{e}})$$
Here , L is the length of microscope tube , f_{0} and f_{e} are the focal lengths of objective and eyepiece respectively and D = 25 cm. It is clear that magnification M of the compound microscope will be large if both $f_{o}$ and $f_{o}$ are small.
(e) The image of the objective lens in the eye piece is called eye ring. All the ray from the object retracted by the objective lens pass through the eye ring. Therefore it is an ideal position for the our eyes for viewing. If we place our eyes to close to the eye piece , we shall not collect much of the light and also reduce our field of you. If we position our eyes on the eye ring and the area of the pupil of our eye is greater or equal to the area of the eye ring , our eyes will collect all the light refracted by the objective lens.
9.26 An angular magnification (magnifying power) of 30X is desired using an objective of focal length 1.25cm and an eyepiece of focal length 5cm. How will you set up the compound microscope?
Solution:
Here , m = 30 , f_{o} = 1.25 cm , f_{e} = 5 cm
We assume that the microscope is in normal adjustment so that the final image is formed at least distance of distinct vision ( D = 25 cm ) from the eyepiece.
Angular magnification of eye piece is
$$M = (1+\frac{D}{f_{e}}) = 1+ \frac{25}{5} = 6$$
Now , total angular magnification is M =
$$M = M_{e} \times M_{o}$$
Angular magnification of the objective lens is
$$M_{0} = \frac{M}{M_{e}}$$
$$M_{0} = \frac{30}{6} = 5$$
As the objective forms the real image.
$$M_{0} = \frac{v_{o}}{u_{o}} = -5$$
$$v_{o} = - 5 u_{o}$$
For objective lens :
$$\frac{1}{v_{o}} - \frac{1}{u_{0}} = \frac{1}{f_{o}}$$
$$\frac{1}{-5u_{o}} - \frac{1}{u_{0}} = \frac{1}{1.25}$$
$$\frac{-6}{5u_{o}} = \frac{1}{1.25}$$
$$u_{o} = - \frac{6 \times 1.25}{5}$$
$$u_{o} = -1.5 cm$$
Therefore, the object should be held at 1.5 cm in front of the objective lens.
$$v_{o} = - 5 u_{o}$$
$$v_{o} = - 5 \times (-1.5)$$
$$v_{o} = 7.5cm$$
For eyepiece lens :
$$\frac{1}{v_{e}} - \frac{1}{u_{e}} = \frac{1}{f_{e}}$$
$$v_{e} = - D = -25 cm$$
$$\frac{1}{u_{e}} = \frac{1}{v_{e}} - \frac{1}{f_{e}}$$
$$\frac{1}{u_{e}} = \frac{1}{-25} - \frac{1}{5}$$
$$\frac{1}{u_{e}} =- \frac{1}{25} - \frac{1}{5}$$
$$\frac{1}{u_{e}} = \frac{-6}{25}$$
$$u_{e} = -25/6 = -4.17cm$$
Separation between the objective and eye piece
$$L = | u_{e}| + | v_{o}|$$
$$L = 4.17+7.5 = 11.67$$
Therefore objective and eyepiece should be placed 11.67 cm apart and the object at a distance of 1.5 cm in front of the objective
9.27 A small telescope has an objective lens of focal length 140cm and an eyepiece of focal length 5.0cm. What is the magnifying power of the telescope for viewing distant objects when
(a) the telescope is in normal adjustment (i.e., when the final image is at infinity)?
(b) the final image is formed at the least distance of distinct vision (25cm)?
Solution :
Here $f_{o} = 140 cm , f_{e} = 5 cm$
(a) In normal adjustment :
In this case , final image is at infinity
Magnifying power ,
$$M = - \frac{140}{5}$$
$$M = -28$$
(b) When final image is at least distance of distinct vision
Magnifying power ,
$$M = - \frac{f_{o}}{f_{e}}(1+\frac{f_{e}}{D})$$
$$M = - \frac{140}{5}(1+\frac{5}{25})$$
$$M = - 28 \times (1 +.2)$$
$$M = -28 \times (1.2)$$
$$M = -33.6$$
9.28 (a) For the telescope described in Exercise 9.27 (a), what is the separation between the objective lens and the eyepiece?
(b) If this telescope is used to view a 100 m tall tower 3 km away. what is the height of the image of the tower formed by the objective lens?
(c) What is the height of the final image of the tower if it is formed at 25cm?
Solution:
(a) Here , the telescope is in normal adjustment
Separation between the objective lens and the eyepiece is
$$L = f_{o} + f_{e}$$
$$L = 140+5$$
$$L = 145cm$$
(b) Angle subtended by 100m tall tower at 3 km away is
$$ \alpha = tan\alpha = \frac{Height \ of \ tower}{Distance \ of \ tower}$$
$$tan \alpha = \frac{100}{3 \times 10^{3}} = \frac{1}{30}rad$$
Let h be the height of the image of tower formed by the objective. Then angle subtended by the image produced by the objective will also be equal to $\alpha$.
$$\alpha = \frac{h}{f_{o}}=\frac{1}{30}rad$$
$$\frac{h}{140}=\frac{1}{30}rad$$
$$h = \frac{140}{30} = 4.67 cm$$
(c) Magnification produced by the eyepiece is
$$M_{e} = 1+ \frac{D}{f_{e}}$$
$$M_{e} = 1+ \frac{25}{5}$$
$$M_{e} = 6$$
Height of final image =
$$M_{e} \times h = 6 \times 4.67 = 28 cm$$
9.29 A Cassegrain telescope uses two mirrors as shown in Fig. 9.26. Such a telescope is built with the mirrors 20mm apart. If the radius of curvature of the large mirror is 220mm and the small mirror is 140mm, where will the final image of an object at infinity be?
Solution :
The image formed by their objective mirror ( concave mirror) acts as a virtual object for the secondary mirror ( convex mirror)
Focal length of the objective concave mirror is
$$f_{1} = -\frac{220}{2} = -110 mm$$
Focal length of the secondary convex mirror is
$$f_{2} = + \frac{140}{2} = +70 mm$$
Distance between the two mirror is d = 20 mm
When the object is at infinity, the objective concave mirror will form the image of the object at its focus F i.e at 110mm from objective mirror . As this image lies behind the secondary convex mirror , it acts as a virtual object for the convex mirror.
For secondary mirror :
$$u = f_{1} -d$$
$$u= 110-20 = 90mm$$
$$f_{2} = 70 mm$$
$$v = ?$$
Using mirror formula
$$\frac{1}{u} + \frac{1}{v} = \frac{1}{f_{2}}$$
$$ \frac{1}{v} = \frac{1}{f_{2}} - \frac{1}{u}$$
$$\frac{1}{v} = \frac{1}{70} - \frac{1}{90}$$
$$\frac{1}{v} = \frac{9-7}{630}$$
$$\frac{1}{v} = \frac{1}{315}$$
$$v = 315mm$$
To the right of secondary mirror
9.30 Light incident normally on a plane mirror attached to a galvanometer coil retraces backwards as shown in Fig. 9.29. A current in the coil produces a deflection of 3.5° of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5 m away?
Solution:
When the plane mirror rotates through angle $\theta$ from position M to $M^{'}$, the reflected ray turns through angle $\2theta$. Therefore, reflected spot moves on the screen from position B to A.
$$\angle BOA = 2\theta = 2 \times 3.5^{o} = 7^{o}$$
From the right angled $\bigtriangleup OBA$ , we have ,
$$tan\2theta = \frac{AB}{BO}$$
$$tan\2theta = \frac{d}{1.5}$$
$$d = 1.5 tan\2theta = 1.5 tan 7^{o}$$
$$d = 0.1842m = 18.42 cm$$
9.31 Figure 9.30 shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0cm. What is the refractive index of the liquid?
Solution :
The liquid between the convex lens and the plane mirror behave as a Plano concave lens.
In the absence of the liquid :
Suppose the liquid is not there this means that convex lens is present while the Plano concave lens formed by the liquid is absent the Ray of light after refraction through the convex lens are reflected by the plane mirror as the needle and its image concide with each other , it means that Ray of the light retrace their path after reflection from play mirror it can happen if the needle lies at the focus of a convex lens. Therefore distance of the needle from the lens is equal to the focal length of a convex lens.
Focal length of the convex lens $f_{1} = 30 cm$
Radius of curvature (R) of the convex lens from lens maker's formula
$$\frac{1}{f_{1}} = (\mu-1) (\frac{1}{R_{1}}- \frac{1}{R_{2}})$$
As the lens is equiconvex , $R_{1} = R$and $R_{2} = -R$. Also $\mu = 1.5$
$$\frac{1}{30} = (1.5-1) (\frac{1}{R}- \frac{1}{(-R)})$$
$$\frac{1}{30} =.5 \times \frac{2}{R}$$
$$\frac{1}{30} =.5 \times \frac{2}{R}$$
$$\frac{1}{30} = \frac{1}{R}
$$R = 30 cm$$
In the presence of liquid
Now both convex lens and Plano concave lens formed by the liquid are present. Now the needle lies as a focus of the combination of two lenses.
Focal length of the combination of lenses
F = 45 cm
Let $f_{2}$ the focal length of the liquid Plano concave lens.
$$\frac{1}{F} = \frac{1}{f_{1}}+ \frac{1}{f_{2}}$$
$$\frac{1}{45} = \frac{1}{30}+ \frac{1}{f_{2}}$$
$$\frac{1}{f_{2}} = \frac{1}{45} - \frac{1}{30}$$
$$\frac{1}{f_{2}} = \frac{1}{-90}$$
$$f_{2} = -90 cm$$
For Plano concave lens
We have
$$f_{2} = -90cm $$
$$ R_{1} = -R = -30$$
$$R_{2} = \infty$$
$$\mu_{l} = ?$$
$$\frac{1}{f_{2}} = (\mu_{l}-1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$$
$$\frac{1}{-90} = (\mu_{l}-1) (\frac{1}{-30} - \frac{1}{\infty})$$
$$\frac{1}{-90} = (\mu_{l}-1) (\frac{1}{-30})$$
$$\frac{1}{3} = (\mu_{l}-1) $$
$$\frac{1}{3} +1 = \mu_{l}$$
$$\mu_{l} = \frac{1}{3} +1$$
$$\mu_{l} = \frac{4}{3}$$
$$\mu_{l} = 1.33$$